前言

  • 你可能会遇到这样的情况
  • 某天，你像往常一样打开电脑，准备撰写文稿，这时，你的一个朋友给你发来一个信息：“Hey！快看看我新编的故事写得怎么样 ？！”，然后就给你发来了一个 .txt 文档
  • 你饶有兴致的接收了这个文档，然后鼠标双击打开了它…

image-20211115144145486

  • 如果你确实遇到了诸如此类修仙三百年也不一定看得懂的文本内容，并且不知道如何处理，那就继续阅读本文吧～
  • 别忘了给你的朋友回复一句：“老哥写得牛批 ！”

我假设你已经看了YOUTUBE上的计算机科学速成课

举个日常生活中的例子

  • 以使用电脑写英语作文为例，我们会连续不断地敲击键盘，向电脑中输入英文字母
  • 当 ctrl+s 保存时，电脑就会将我们输入的这些英文字母所转换成的 0 和 1 们存储到我们电脑的硬盘中
  • 当下次再打开这个英语作文时，电脑就会从硬盘中读取出上次保存的这些 0 和 1，并将它们转换回正确的英文字母，进而显示到屏幕上

什么是 「编码、解码」 ？

  • 在上面这个例子中

    • 英文字母被转换成一堆 0 和 1 的过程就被称为编码
    • 这些 0 和 1 被转换回英文字母的过程就被称为解码

  • 可以用数学中的 「函数与反函数」 的知识来理解 「编码与解码」，基于上面这个例子

    • 将英文字母看作自变量，通过某种编码方式（映射方式）就能得到一堆 0 和 1
    • 将这堆 0 和 1 看作自变量，通过解码方式（编码方式的反函数）就能得到正确的英文字母

文件乱码的处理方式

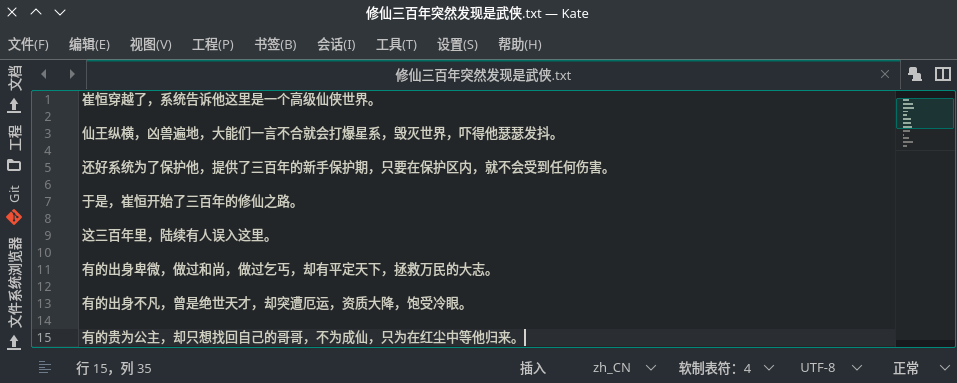
  • 所以：
    • 文件乱码的原因，就是所选的编解码方式错误，比如文章开头图片中的编解码方式显示在右下角，是 UTF-7，其实只需更改为正确的编解码方式 UTF-8 即可

image-20211115172050165

以下为补充知识

固定长度编码 & 可变长度编码

  • 固定长度编码：每个字符用相等长度的二进制位表示
  • 可变长度编码：不同字符允许用不等长的二进制位表示

对一个英文字母进行固定长度编码，它占几个 bit ？

  • 计算机中的一个 「位（bit）」 可以存 0，也可以存 1，就是说一个位能区分两种状态

  • 一共有 26 种英文字母，就需要用 0 和 1 来区分表示 26 种状态，显然需要更多的位

  • 2^4 = 16，2^5 = 32，16 < 26 < 32，所以需要至少 5 个 bit 才能区分表示出 26 种状态

  • 为了使用方便，我们规定用 1 Byte 的空间存储一个英文字母，即一个英文字母编码后，所占的空间大小为 8 bit（考研默认每个字符占 8 位）

字符集的概念

  • 英文字符少，每一个英文字符都包含于 => ASCII字符集
  • 中文字符多，每一个中文字符都包含于 => Unicode字符集

备注

  • 对于同一个字符集，可以采用不同的编解码方式，如 UTF-8、UTF-16…
  • 对一个字符采用不同的编码方式进行编码，所得的二进制数所需的存储空间大小是不一样的

以下为进阶知识，涉及 「哈夫曼树（最优二叉树）」、「哈夫曼编码（适用于数据压缩）」

从一个例子看 「固定长度编码的缺陷」

  • 小渣和老渣是计算机系的两个学生，他们也学习了编解码的知识，于是打算在期末考试中用编解码的知识打暗号作弊（Tips：考试作弊已入刑法，违法必究）

  • 他俩的思路是这样的：

    • 选择题一共有 A、B、C、D 四个选项
    • 将这四个选项进行二进制编码，得到答案选项的二进制表示
    • 用 「咳嗽」 表示 0，用 「打嗝」 表示 1
    • 然后就可以用连续的咳嗽和打嗝来传递信息，经过解码，答案就出来了

  • 若采用固定长度编码：

    • 一共有 A、B、C、D 四种选项，要用 0 和 1 区分出这四种状态，每个答案选项就至少需要用 2 个 bit 来表示
    • 比如
      • A <=> 00
      • B <=> 01
      • C <=> 10
      • D <=> 11

  • 怎么用呢 ？

    • 比如小渣要把 100 个答案传给老渣，小渣的答案中有（80 个 C、10 个 A、8 个 B、2 个 D）
    • 那他一共需要传递 80 * 2 + 10 * 2 + 8 * 2 + 2 * 2 = 200 个二进制位
    • 也就是需要咳嗽和打嗝 200 次，才能传完答案（监考老师热心关怀的概率：100%）
    • 小渣打了个冷颤，开始思考如何让传递的二进制位的个数尽可能地少

分析这种缺陷的原因

  • 上面这种固定长度编码的方式可以用 「树」 来表示

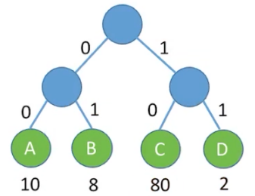
image-20211115185423296

  • 80 * 2 + 10 * 2 + 8 * 2 + 2 * 2 = 200 正好是树的带权路径长度 WPL
  • 于是问题就转化为了 「如何让二叉树的带权路径长度最小」 ？

最优二叉树（哈夫曼树）

让二叉树的带权路径长度最小 ？

小渣灵光一现，构建最优二叉树 ！（哈夫曼树 ！）

明确：哈夫曼树（最优二叉树）不唯一 => 哈夫曼编码不唯一

  • 把选项看作结点
  • 把选项出现的频度看作结点的权值
  • 用这 4 个带权结点构建最优二叉树（哈夫曼树）
  • 这样就得到了 WPL 最小的树，也就得到了一套哈夫曼编码（属于可变长度编码）
  • 能够确保传递的二进制信息最少（即实现了数据压缩）
  • 哈夫曼编码属于 「前缀编码」，即没有一个编码是另一个编码的前缀（否则传递的数据会有二义性）

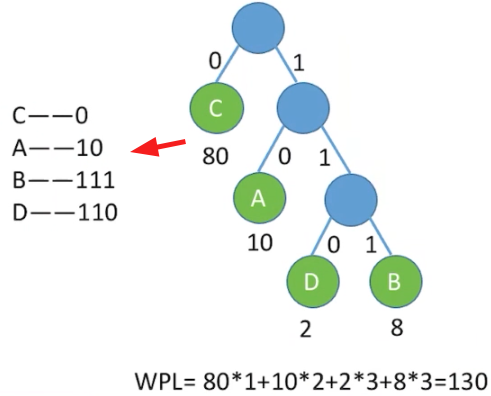
image-20211115190829597

  • 相比于之前的 200 次，若采用哈夫曼编码，小渣只需咳嗽打嗝 130 次，就可以传递 100 个答案，还是十分搞笑的

哈夫曼编码广泛用于数据的压缩

  • 比如 26 个英文字母的使用频率是不同的，对于一段英文，如果它采用的是 ASCII 编码（属于固定长度的编码）
  • 那么就可以将这段英文采用哈夫曼编码（用这 26 个权值不同的结点构建哈夫曼树，可得哈夫曼编码）进行重新编码
  • 就实现了数据压缩

image-20211115120514176

以下为数据结构专业知识 ～ 哈夫曼树（最优二叉树）

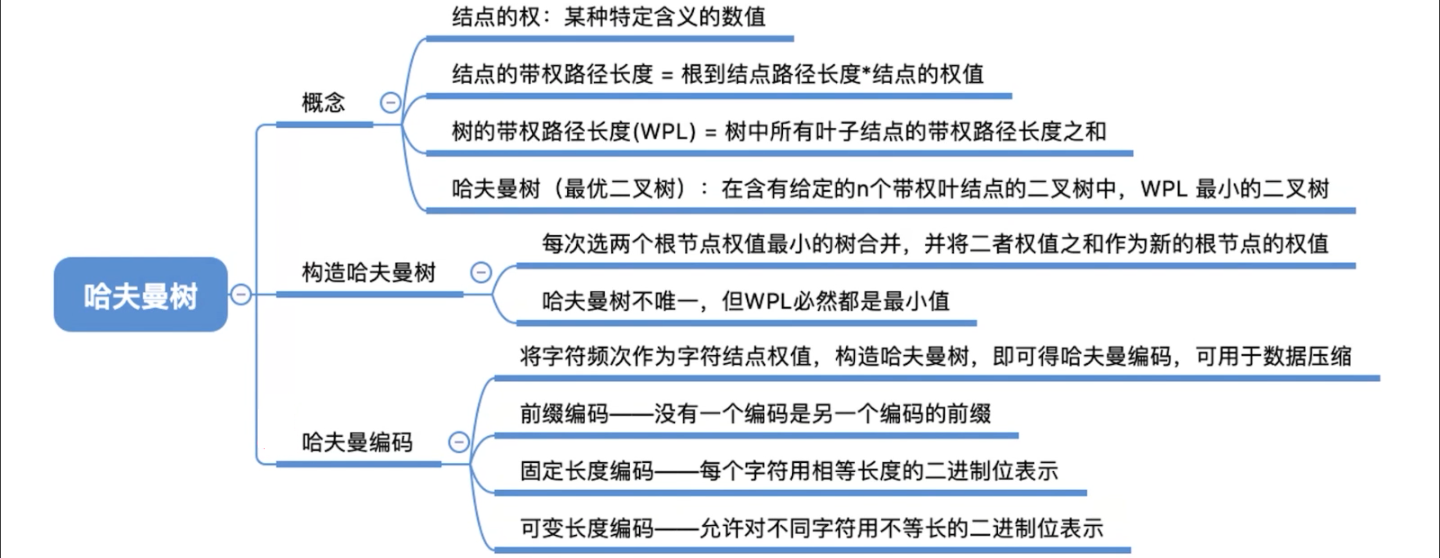
啥叫 「结点的权」 ？

  • 有某种现实含义的数值，比如表示结点的重要性等

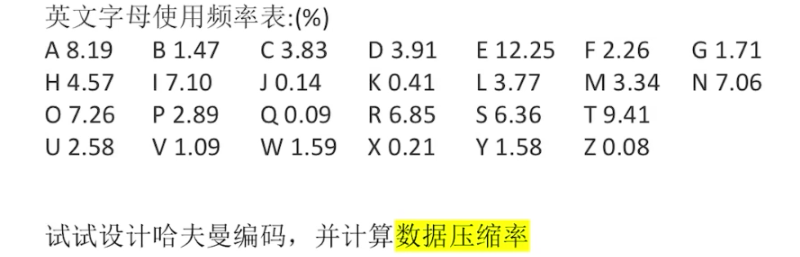
啥叫 「结点的带权路径长度」 ？

  • 从根结点到该结点的路径长度 * 该结点的权值

啥叫 「树的带权路径长度」 ？

  • 树中所有叶子结点的带权路径长度之和（WPL, Weighted Path Length）

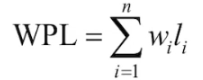
image-20211114203648441

image-20211114203933185

啥叫 「哈夫曼树」 ？

  • 含有 n 个带权叶结点，且带权路径长度（WPL）最小的二叉树被称为哈夫曼树，也叫最优二叉树

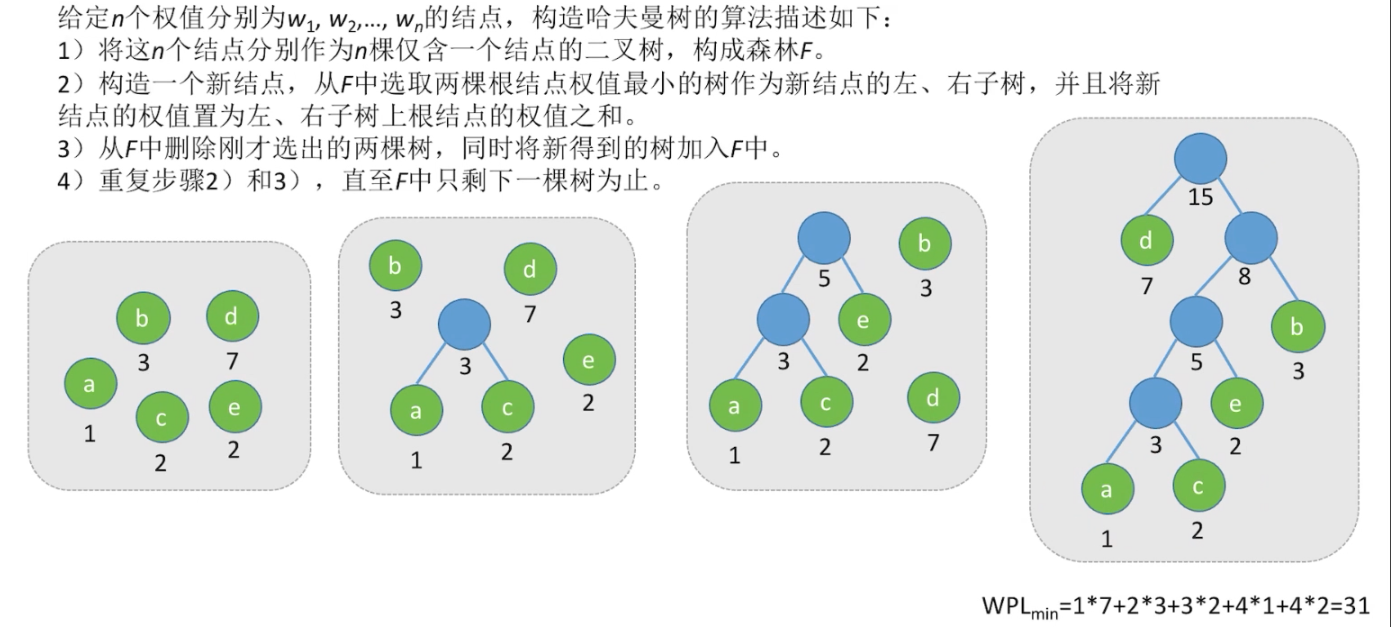
给出一堆带权叶结点 => 如何构造哈夫曼树 ？

步骤 2 左右子树顺序任意~

image-20211114205005741

哈夫曼树的特点

  • 哈夫曼树中，结点的度为 0 或 2，不存在度为 1 的结点
  • 每个初始结点最终都成为叶结点，且权值越小的叶结点到根结点的路径长度越长
  • 由于每执行一次步骤 2 都会向哈夫曼树中新增一个结点，初始给定 n 个叶子结点，那么就会执行 n-1 次步骤 2，所以最终哈夫曼树中会有 n+(n-1) 个结点
  • 哈夫曼树不唯一 => 哈夫曼编码不唯一，但 WPL 必定相同且为最小值（最优）！

哈夫曼树小结

image-20211115120409324

（完）